1. NURBS (Non-Uniform Rational B-Spline) - Alguns conceitos iniciais

Atualmente, os sistemas CAD classificados como modeladores de superfícies permitem a construção de formas complexas, dando ao usuário total liberdade para o modelamento de seus produtos. Um sistema CAD com estas características possui sofisticados modelos matemáticos que possibilitam representações geométricas complexas

Estes algoritmos matemáticos são conhecidos como funções Spline. "Spline é uma curva não-concêntrica, não-reta e desenhada suavemente através de uma série de pontos, conhecida também como curva francesa".
Estes modelos matemáticos foram desenvolvidos inicialmente por Lagrange, Hermite e mais recentemente pelo francês Paul Bézier, que utilizou em 1972 sua formulação no sistema Unisurf, para representar formas complexas de um painel de carro produzido pela empresa na qual trabalhava, a Renault.

Esta foi a primeira utilização de sistemas computacionais para modelamento de superfícies em projetos mecânicos. Atualmente, a formulação proposta por Bézier sofreu algumas alterações, surgindo os modelos B-Spline e a mais recente NURBS (Non-Uniform Rational B-Spline), permitindo maior manipulação e controle da curva ou superfície gerada, e conseqüentemente, maior versatilidade na representação de formas complexas.
A seguir, encontra-se uma breve descrição das principais metodologias Spline utilizadas para a representação de curvas complexas em sistemas CAD. A representação de superfícies complexas é uma extrapolação do conceito utilizado para a representação de curvas complexas. Todas as metodologias descritas a seguir utilizam-se equações polinomiais paramétricas para a representação das curvas. As variáveis X, Y, e Z estão em função de um único parâmetro.

2. Curvas de Hermite
Sendo uma das primeiras representações matemáticas de curvas complexas, Hermite definiu uma curva utilizando uma equação polinomial, dois pontos e dois vetores tangentes que determinam sua forma, como ilustra a Figura 1.
A curva proposta por Hermite é definida por um polinômio e pontos de início e fim, associados a dois vetores, o que permite um controle razoável sobre a curva. A utilização e edição dos pontos e dos vetores tangentes são úteis para o modelamento de formas complexas.

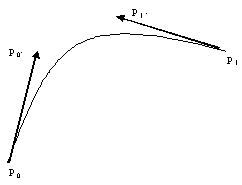
Figura 1: Curva de Hermite

No entanto, utilizando a metodologia de Hermite, os valores dos pontos e as inclinações dos vetores devem ser atribuídos numericamente, dificultando a utilização prática desta técnica.

3. Curvas de Bézier
Visando eliminar as inconveniências da formulação de Hermite, Bézier utilizou-se de um polígono para definir a curva, substituindo os pontos e os vetores utilizados por Hermite, como ilustra a Figura 2. Este polígono é aproximado por uma equação polinomial paramétrica, baseado na equação a seguir:

onde:
P é o ponto da curva (x;y;z) representada pelo polígono P1 à P4,
U é o valor paramétrico variando de 0 a 1

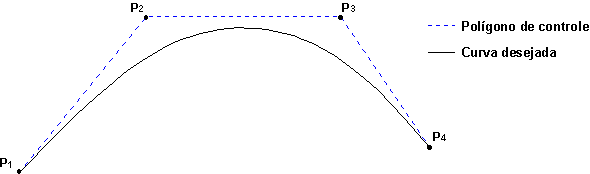
Figura 2: Representação de uma curva através de um polígono de controle

Os pontos do polígono atraem a curva, permitindo manipulações interativas. As modificações na curva são realizadas pela edição dos pontos que definem o polígono de controle. A curva passa pelo primeiro e último ponto e são tangentes ao primeiro e ao último segmento do polígono de controle. Um dos inconvenientes desta metodologia é que apenas permite modificações globais da curva. A alteração de um ponto do polígono, altera-se a curva toda.
Uma evolução das curvas de Bézier é a representação B-Spline, que se utiliza também de uma equação polinomial paramétrica e pode ser considerada como uma generalização das curvas de Bézier, com algumas modificações, permitindo entre outras coisas, representar uma curva utilizando-se um polinômio de baixo grau, facilitando os cálculos computacionais, permitindo também modificações locais da curva.

4. Curvas NURBS
Basicamente, a metodologia NURBS (Non-Uniform Rational B-Spline) baseia-se na metodologia B-Spline, acrescentando duas funções principais:

Algoritmos NURBS permitem um controle mais apurado sobre a geometria, além da possibilidade de representar uma curva complexa utilizando-se um polinômio de baixo grau. Em síntese, estas características significam que mais fatores de controle podem ser aplicados à curva, de modo que superfícies mais complexas possam ser representadas com um menor número de curvas. Por estas razões, a metodologia NURBS se tornou a mais eficiente para a representação de curvas e superfícies complexas.

5. Trajetórias de ferramenta
O método mais utilizado para descrever a trajetória de ferramenta para usinagem de superfícies complexas é a interpolação linear de segmentos de retas, utilizando comandos G01. Existem outras metodologias, como a interpolação circular/linear e interpolações tipo Spline, neste caso, para descrever uma trajetória complexa de ferramenta. Por serem relativamente recentes, estas duas metodologias ainda são pouco estudadas.
O programa NC gerado utilizando um método Spline não irá conter os comandos tradicionais, G01, G02 ou G03, mas uma nova codificação, como ilustrar as linhas de programa a seguir:
...
N4 G43 Z27.822 H00
N5 Z11.1
N6 G01 Z-2.075 M08 F4000.
N7 POLY PO[X]=(-2.446 ,-.012 ,.006) PO[Y]=(0.,0,0) PO[Z]=(-1.851 ,-.031 ,.012)
N8 PO[X]=(-2.393 ,.005 ,-.001) PO[Y]=(0.,0,0) PO[Z]=(-1.643 ,.004 ,-.001)
N9 PO[X]=(4.469 ,4.219 ,-.538) PO[Y]=(0,0,0) PO[Z]=(8.291 ,-1.168 ,-.792)                              .....

Figura 3: Linhas de um programa NC em formato polinomial

A Figura 4 ilustra as três técnicas de interpolações, utilizadas para descrever uma mesma trajetória de ferramenta

Figura 4: Métodos para descrever trajetórias de ferramenta e geometrias complexas

Os dois últimos tendem a propiciar melhores resultados de usinagem, reduzindo o tamanho dos programas NC gerados, com a possibilidade de se trabalhar com maior velocidade de avanço, reduzindo o tempo de usinagem. Outro fator já documentado, é a possibilidade de se obter melhor qualidade na superfície usinagem, utilizando-se interpolações NURBS ou circular/linear.

   MSc Eng. Adriano Fagali de Souza