Definições
de matrizes
(conforme linguagem APT que também usado como arquivos fontes
gerados em sistemas CADCAM)
Desde que dimensionar em um desenho de engenharia normalmente independente
do sistema de coordenada da máquina ferramenta na qual a
peça será usinada, os programadores consideram que
embora as dimensões possam ser suficientes para definir as
várias linhas, círculos, pontos, etc., é difícil
de fazer no sistema de coordenada da máquina.
Os comandos REFSYS, TRACUT, e COPY permitem o programador trabalhar
no sistema de coordenada mais conveniente (por exemplo, um cuja
origem é um ponto de referência no desenho), e então
facilmente especificar uma transformação no sistema
da máquina.
Para propósito de discussão, tal sistema de coordenada
será conveniente chamado de "sistema local". O
sistema global, normalmente da máquina, será chamado
de "sistema básico".
Esta transformação pode consistir em qualquer combinação
de rotações, translações, imagens de
espelho e fatores de escala, e é especificado através
de uma sentença de definição de MATRIZ. Tais
transformações sempre podem ser representadas por
três equações da forma:
A11x1
+ a12y1 +a13z1 +a14 = xb
A21x1 + a22y1 +a23z1 +a24 = yb
A31x1 + a32y1 +a33z1 +a34 = zb
Quer
dizer, para este tipo de transformação, é possível
determinar coeficientes, (a11, a12,…, a34), tal que, para um
determinado ponto com coordenadas (X1, Y1, Z1) no sistema local,
as equações os transladam as coordenadas transformadas
(Xb,Yb,Zb), no sistema básico.
A transformação é chamada como uma 'matriz'
porque este termo é descritivo de forma na qual as três
equações são representadas interiormente pelo
processador N/C, como uma ordem dos coeficientes:
A11
a12 a13 a24
A21 a22 a23 a24
A31 a32 a33 a34
As
notações de dupla-subscrição são
bastante comuns em matemática de matriz. Note que esta mostra
a linha e coluna de um elemento da matriz. Por exemplo, a23 esta
na segunda linha e terceira coluna.
A matriz de transformação revela os atributos geométricos
do sistema de coordenada local, em termos do sistema básico,
diretamente. Suas primeiras três colunas representam os eixos
do sistema local: (a11, a21, a31) é o eixo X de vetor positivo,
(a12, a22, a32) o eixo Y de vetor positivo, e (a13, a23, a33) o
eixo Z eixo de vetor positivo.
A quarta
coluna (a14, a24, a34), é o ponto de origem do sistema local.
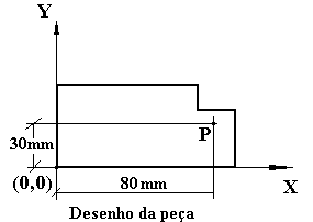
Figura
1 mostra o desenho da peça; o eixo maior da peça é
paralelo ao eixo de X.
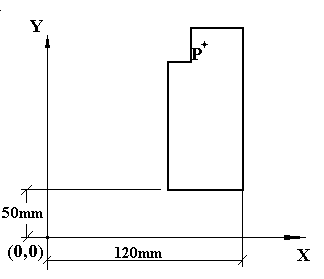
Figure
2 mostra a orientação da peça na máquina;
o eixo maior da peça é agora paralelo ao eixo de Y.
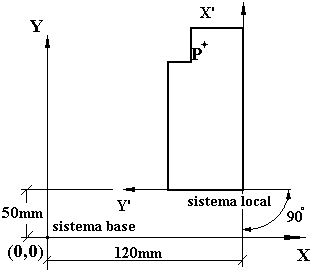
Figure
3 mostra a relação entre os sistemas de coordenada
da base (máquina) e local (desenho da peça).
A transformação
necessitou que todas as entidades, dimensionados nos termos do sistema
local terá dimensões apropriadas no sistema básico,
é uma combinação de 90 graus de rotação
seguida por translação de: 120 mm em X, 50mm em Y,
e 0mm em Z.
A sentença abaixo define "uma matriz definida como uma
combinação ordenada de duas determinadas matrizes".
M1= MATRIX/XYROT, 90,TRANSL, 120,50,0
Gera a matriz
0 -1 0 120
1 0 0 50
0 0 1 0
Que efetuará esta transformação. Por exemplo,
considere o ponto P que tem coordenadas locais (80,30,0). Suas coordenadas
de sistema básico podem ser computadas por:
Xp = 0(80) + (-1)(30) + 0(0) +120 = 90
Yp = 1(80) + 0(30) + 0(0) +50 = 130
Zp = 0(80) + 0(30) +1(0) +0 = 0
O programador da peça especifica P em termos de suas coordenadas
locais (80, 30, 0) e invocando a matriz, M1, com o comando: TRACUT,
COPY, ou REFSYS, isto faz o processador CNC executar a transformação
que se rende às coordenadas básicas (90, 130,0).
Com referência para figurar 3, pode verificar o leitor que
as colunas da matriz contêm: os vetores de eixo e a origem
apontam do sistema de coordenada local, como previamente declarado.